Spirometry is the most frequently performed pulmonary function test for management of diseases affecting the lungs [1]. Unlike most other laboratory parameters that have fixed normal values for all children in population, there are none for spirometry. Normal expected values in a given child are calculated from age and physical measurements using prediction equations developed in studies on normal healthy subjects. The values of parameters measured in a patient are compared with these expected normal values (labelled as predicted) and, if found less than the lower limits of normal, are considered as abnormal or reduced. Correct interpretation mandates that data of Indian children be compared with prediction equations developed in healthy Indian population [1]. Though several equations have been developed from time-to-time for children in different regions of India [2-9], most of these are now outdated and have limited utility due to technological advances in equipment and revisions in methodology. No equations have been developed in India following the last revision of the American Thoracic Society-European Respiratory Society (ATS-ERS) spirometry guidelines [10].

Recently, we presented linear regression equations for spirometry for children of northern Indian origin [11]. However, the increase in lung function with age is non-linear due to the pubertal spurt in height [12,13], and non-linear prediction equations may, therefore, be physiologically more appropriate. The currently recommended equations for Caucasian children in the United States (US) and Europe are non-linear [14,15]. Therefore, in this study, we reanalyzed our data to examine if nonlinear models offered an advantage and compared our predictions with those by Caucasian and previously published Indian equations.

Statistical analysis: Statistical analysis was carried out using SPSS 20.0 (SPSS Inc. Chicago, USA) and Graph Pad Prism 4.01 (Graph Pad Inc. USA) software. Data of male and female participants were analyzed separately. Univariate regression was carried out to identify significant predictors among height, age and weight for the spirometry variables followed by multiple regression analysis. Both linear and nonlinear models were examined. The independent variables were entered into the prediction model in sequence if the R2 improved substantially by more than 1%. Log or other transformations of dependent and/or independent variables were carried out to obtain the best model. Final models were selected on the basis of the highest predictive capability (highest coefficient of multiple determination, R2) and compliance with the requirements of valid regression analysis i.e. independence of predictors, homoscedasticity, and normal distribution of residuals.

Acceptable flow-volume curves were obtained in 365 boys and 305 girls. The demographic characteristics of the study population were described in detail in our earlier communication [11]. The mean (SD) ages and the anthropometric data in boys and girls, respectively were: age (y), 11.74 (3.23) and 11.53 (3.37) (P>0.05); height (m) 1.45 (0.14) and 1.49 (0.18) (P<0.01); weight (Kg) 40.97 (13.82) and 44.56 (18.42) (P<0.01).

TABLE I Prediction Equations for Spirometry Parameters in Boys and Girls

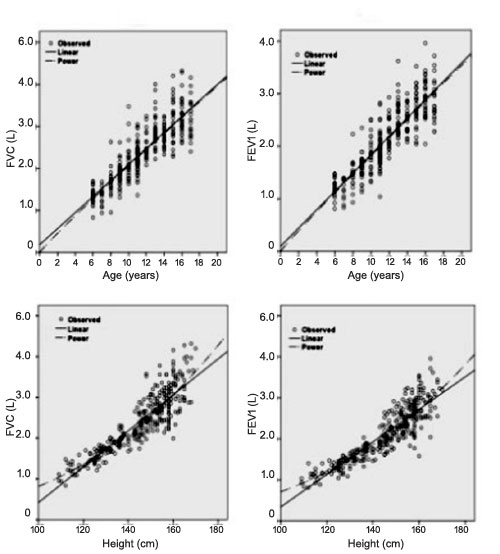
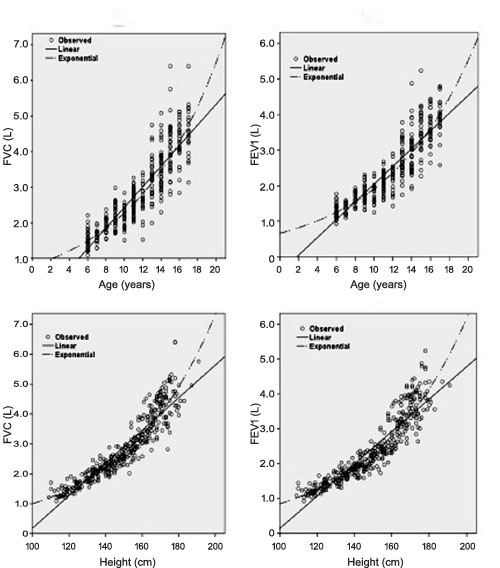
The results of linear and nonlinear regression of FVC and FEV1 against age, height and weight are shown in Web Table 1 and plots against age and height with best-fitting regression lines in girls and boys are shown in Fig. 1 and 2, respectively. Nonlinear lines fitted the observed data better than linear. The final regression equations for all parameters on multivariate analysis are presented in Table I. Height and age were the significant predictors for all parameters. Addition of weight did not result in significant improvement in R2 for any parameter except for FVC in girls where it increased from 0.87 to 0.88. Both equations for FVC, with and without the weight variable are shown. However, the predicted values with the two equations were not significantly different. Nonlinear regression yielded uniformly substantially greater R2 values compared to linear models except for FEF50 for girls where linear equation was retained. The linear models for all other parameters were also rejected because of non-normal distribution of residuals. No statistically valid equation was developed for FEV1/FVC ratio due to lack of significant relationship with any independent variable.

Fig. 1 Linear and nonlinear regression of FVC against (a) age and (c) height, and of FEV1 against (b) age and (d) height in girls.

Fig. 2 Linear and nonlinear regression of FVC against (a) age and (c) height, and of FEV1 against (b) age and (d) height in boys.

Discussion

The present article presents prediction equations for spirometry parameters for children of northern Indian origin between the ages of 6 to 17 years. On multivariate regression analysis, height and age were found to be the main determinants for all parameters in both genders with weight not making any significant contribution to the predictions. The presented equations are nonlinear, and we considered these as superior to the linear equations published by us earlier [12], with greater explained variance. In addition, the residuals were normally distributed with nonlinear equations but not with linear equations.

Most studies from India and other countries have reported linear prediction equations for sake of simplicity and ease of manual calculations [2-4,6-9,20,21]. However, the increase in FVC and FEV1 through childhood is nonlinear with the adolescent growth spurt causing an accelerated increase [13,14]. This relationship was confirmed in our study. Therefore, linear models may not be physiologically appropriate. Gupta, et al. [5] reported that exponential models were not only statistically valid but also fared better than the linear models in Indian children. The equations currently recommended for Caucasian children in the US [14] and Europe [15], and for Singaporean children [22] are also nonlinear. We recommend the application of nonlinear equations to interpret spirometry data in children because these are physiologically appropriate, statistically valid and have a higher explained variance compared to linear equations. Though nonlinear equations are more difficult to compute manually, modern lung function equipments are computerized and therefore this is not a limitation.

The present study has important clinical information for pulmonologists and general pediatricians intending to carry out spirometry in clinical practice and research. As interpretation of measured spirometry data requires a comparison with expected or predicted values in normal population, selection of the correct prediction equations is a critical step [1]. The software of computerized spirometers that are generally used in India usually do not provide any Indian equations because the available ones [2-9,21] have become outdated by current technological and methodological advances. Therefore, equations for other populations, usually Caucasian, have to be used as a substitute. Use of equations developed in other populations is however not advisable for interpreting data of Indians as it is likely to lead to substantial errors and thus adversely affect management decisions [1,23]. This occurs because the Caucasian and Indian predictions of normal values differ substantially. Interpretation algorithms for spirometry are based on FVC and FEV1 [1,20] and the predictions for these by our equations are about 10% less compared to the predictions by the US Caucasian equations [14]. Clinically significant errors in interpretation on using Caucasian instead of Indian equations has been shown in adults [23]. The present study thus addresses a long-felt unmet need in spirometry testing in Indian children in clinical and research studies by providing prediction equations that are appropriate for the local population. These equations can now be incorporated in spirometry software.