All study designs in medical research, barring descriptive studies, involve comparative analysis to achieve its objective/s. Comparisons between groups based on outcomes, or risk factors, or interventions, are the basis of hypotheses in evidence-based medicine. Statistical tests support in making criterion-based decisions about the validity of the hypothesis. A basic knowledge of statistical comparisons helps medical researchers to apply valid statistical tests. Novice medical researchers struggle to decide when, and which statistical test must be applied. There is a need to further reduce the mathematical jargon in statistics related publications for medical researchers. In this article, we aim to provide the readers with practical pointers about the applied aspects of basic statistical comparisons in medical research.

Keywords: Analysis of Variance, Biostatistics, Chi-square distribution, Nonparametric tests, t-test, Hypothesis testing.

The choice of a particular statistical test for analysis depends on the objectives of the study. As the objectives are decided in the protocol, the statistical tests are also chosen at this time itself. One needs to determine whether a statistical test is needed for a research objective, and if yes, then which statistical test is best suited. Inexpe-rienced researchers are often confused while choosing the appropriate statistical test to examine the hypothesis. Most published articles are directed towards describing the various statistical tests, rather than explaining how to choose the appropriate statistical test [2,3]. Those which deal with application of statistical tests are often focused on related issues (including the mathematical equations) such that there is a reduced focus on the basic theoretical concepts which would have helped to understand the principles of selection of the respective test [4,5].

This article aims to provide practical tips to novice researchers to approach the application of basic statistical tests for comparing groups in medical research.

Statistical tests are used to test hypotheses. Hypothesis is a prediction about a new phenomenon. It makes a statement about the existence of a relationship or effect of a factor on a phenomenon [6]. The objectives which are descriptive in nature, rather than comparative, have no hypothesis to test, and do not need of any statistical test. The researcher just wants to see what is there rather than to compare [7]. In case of more than one objective, statistical tests may be applicable on certain objectives but not on others.

Let us consider the following objectives: i) To estimate the proportion of children who are completely vaccinated in a given community; and ii) To determine the effect of an educational intervention on child immunization coverage in a given geographical area. The first objective does not intend to predict anything or does not state any possible relationship or effect of a factor on a phenomenon and therefore, is not a hypothesis statement. Hence, no statistical test will be needed for this objective. The second objective tries to find the impact of factor X (educational intervention) on phenomenon B (child immunization coverage). This being a hypothesis statement, will require a statistical test.

For hypothesis testing, the statistical tests attempt to reject the null hypothesis. Null hypothesis makes the assumption that there is no difference between the two groups or there is no relationship between the two variables. We apply statistical tests to find whether the null hypothesis is true or false. The P value obtained from a statistical test is the probability that both the groups come from the same population rather than two different populations. In simple terms, it is the probability that the difference observed between the two groups is a chance finding. The lower the P value, the lesser the probability that the observed difference is by chance [8]. Statistical tests either reject or accept the null hypothesis, depending on whether the P value is less than 0.05 or more than or equal to 0.05, respectively [9].

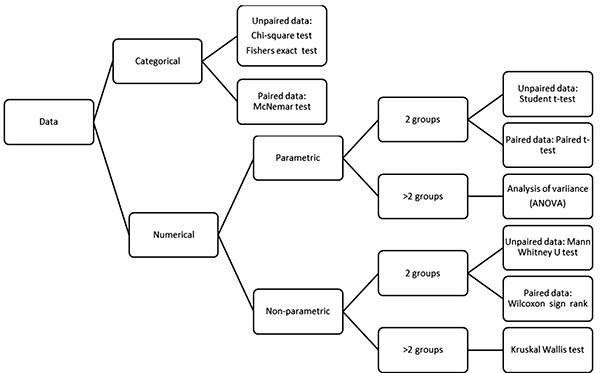
An algorithm to choose an appropriate statistical test for comparison is given in Fig 1. Parametric tests require estimation of variables that define the underlying distribution of data, like mean and standard deviation for normally distributed data [10]. Simply put, when means are compared, the tests used are known as parametric, whereas for comparison of medians or categorical variables, the tests used are referred to as nonparametric.

Fig. 1 Algorithm to decide the appropriate statistical test in medical research.

When variable X is compared between two (or more) groups, we decide about the type of data and whether data are paired or not.

The first step is to ascertain the type of data being compared. For most practical purposes, data can be considered as categorical or continuous [11]. A variable such as sex (male/female) or intensity of pain (mild, moderate, severe) where responses will be grouped in one or more categories are categorical variables. They are called nominal when there is no order or grade, and ordinal when they are graded or ordered. Continuous data are those where each observation gets a score. It can be an interval data wherein there is no absolute zero like intelligence quotient scores or temperature in Celsius or ratio data or when an absolute zero exists like heart rate, number of episodes of diarrhea and age.

Continuous data can be transformed to categorical data by applying cut-offs e.g., hemoglobin level is continuous data, but can be converted into categorical data i.e., anemic and non-anemic by applying cut-offs for classifying anemia. However, such conversions must be avoided because it leads to a loss of data, and also reduces the power. Dichotomization leads to loss of variability and dichot-omizing at the median value leads to loss of power by one-third. The values near either side of the cut-off, go far away in two categories in this conversion [10]. Care should also be taken to choose appropriate cut-off points. It is preferable to use already recognized cut-offs or they should be justified and decided a priori, before the beginning of the study.

Quantitative data should be decided and mentioned a priori, whether they will be considered as continuous or categorical data for the purpose of statistical analysis.

The second step to decide about the statistical test is to find out whether the data is paired or unpaired. Data is considered to be paired if: i) Two measurements are taken from the same individual either at two different time points e.g., before and after an intervention or exposure; or at the same time but for two different tests to be compared e.g., when comparing two or more diagnostic tests; ii) Measurements are taken from pairs of subjects which have been matched at the time of inclusion; and iii) Data from siblings and twins are also considered as paired [13].

Data such as sex (male or female); disease status (diseased or healthy) and risk factor (present or absent) is categorical in nature. The frequency distribution of two or more categorical variables is presented in a matrix format called as contingency tables or crosstabs.

Pearson chi-square or just chi-square test is applied to compare this kind of data. Being a non-parametric test, it is robust with respect to the distribution of data. Even though there is no limit on the number of rows and columns, to meet the assumptions of chi-square test and for ease of interpretation, too many cells must be avoided [14]. For each cell in a contingency table, expected cell count can be calculated by the product of row total and column total, divided by the grand total. The assumptions for chi-square test are given in Box I.

Mc Nemar test should be used, while comparing paired categorical data [15]. Chi-square test is also not helpful when the numbers in the table are small. In such instances, Yate correction or Fisher exact test is applied. A general rule of thumb to apply Yate correction is when the sum of all the values in the cells is less than 100 or the value in any one cell is less than 10 [16]. In contingency tables, if more than one-fifth of the cells the expected values are less than 5, chi-square test is inappropriate and Fisher exact test may be more appropriate [16]. When reporting results of a chi-square test the style of individual journal should be checked – at Indian Pediatrics, we only ask that the P value must be reported.

Quantitative variables may be of various types such as discrete or continuous, as described previously, and ratio or interval (not described here). Usually these are summarized as mean or median, for normally and non-normally distributed data, respectively. The distribution of data can be checked either by generating a histogram and examining it visually or by using a statistical test such as Shapiro-Wilk test. A quick (but less accurate) way to assess the normality of data is to compare the mean and standard deviation (SD). If mean is nearly similar to median and the mean is more than 2-3 times of SD, then it can be considered ‘normally distributed’. However, this should only be used when sample size is more than 50 [17,18].

Even for ordinal data or non-normal distribution, with a reasonably large sample size, parametric tests can be used. A rule of thumb states that while comparing 2-9 groups if each group has more than 15 observations then the sample is sufficiently large [19].

While choosing tests, another parameter to consider is the equality of variances in the two groups. This can be checked by Levene test. Parametric tests are best when the variances in the two groups to be considered are equal. Even when one variance is up to 2-3 times the other, parametric tests can be used. However, if the difference in variances is greater, a parametric test is no longer valid.

For comparing quantitative data between two groups, the parametric tests used are Student t-test (for unpaired data) and paired t-test (paired data). For more than two groups, Analysis of Variance (ANOVA) is the appropriate test to use. While applying the Student t-test or ANOVA some assumptions must be met as given in Box II.

Parametric tests are preferred because of higher statistical power as they have a greater chance to detect a statistically significant difference, if a difference actually exists [20]. In cases where data are not normally distributed, an attempt can be made to transform it (to normal distribution), so that a parametric test may become applicable. Taking natural logarithms (log transformation) or squares of values are some methods that can be used to transform data. For larger studies (sample size >200), parametric tests can and should be used even for skewed data [21]. While reporting a result of a t-test, its important to mention the number of observations in each group, the mean and SD of each group, and the P values associated with it.

The non-parametric equivalent (to compare medians) are Mann-Whitney U-test (unpaired data) and Wilcoxon sign rank test (paired data). When comparing between more than two groups, Kruskal Wallis test is the non-parametric equivalent of the parametric analysis of variance (ANOVA).

This article focuses on bivariate analysis. Multivariate analysis which adjusts for the confounding effects of the independent variables or the predictors is beyond the scope of this article. Bivariate analysis often helps to identify variables for developing multivariable regression models. The statistical tests used to compare sensitivity and specificity etc. in diagnostic studies are also based on the principles described in the article.

Comparisons of data points using statistical tests form an important aspect of hypothesis testing in evidence-based research. The type and distribution of data, and pairing status, are helpful to decide the appropriate statistical test (Box III). The algorithm presented in the paper will be helpful in decision making. Chi-square, Student t-test, Mann Whitney U test, and ANOVA are some of the statistical tests used commonly in medical research. The assumptions for the tests must be met when applying a particular statistical test.

Funding: None; Competing interest: None stated.

1. Röhrig B, du Prel JB, Wachtlin D, Blettner M. Types of study in medical research: Part 3 of a series on evaluation of scientific publications. Dtsch Arztebl Int. 2009;106:262-8.

2. Thomas E. An introduction to medical statistics for health care professionals: Basic statistical tests. Musculoskelet Care. 2005;3: 201-12.

3. Ali Z, Bhaskar SB. Basic statistical tools in research and data analysis [published correction appears in Indian J Anaesth. 2016;60:790].　Indian J Anaesth. 2016;60:662-9.

4. Nayak BK, Hazra A. How to choose the right statistical test? Indian J Ophthalmol. 2011;59:85-6.

5. Marusteri M, Bacarea V. Comparing groups for statistical differences: How to choose the right statistical test? Biochem Med (Zagreb). 2010;20:15-32.

6. Price PC, Jhangiani R, Chiang ICA. Developing a hypothesis. In: Research Methods in Psychology. Pressbooks, 2017. Accessed July 29, 2020. Available from: https://open text.wsu.edu/carriecuttler/chapter/developing-a-hypothesis/

7. Swinscow TDV.　Study design and choosing a statistical test. In: Statistics at Square One 9th Ed (Revised by MJ Campbell) BMJ Books, 1996.

8. Goodman SN. P value hypothesis and likelihood: Implications for epidemiology of a neglected historical debate.　Am J Epidemiol.　1993;137:485-96.

9. Indrayan A, Satyanarayana L. Basic philosophy of statistical tests, confidence intervals and sample size determination.　Indian Pediatr. 2000;37:739-51.

10. Whitley E, Ball J. Statistics review 6: Nonparametric methods. Crit Care. 2002;6:509-13.

11. Swinscow TDV.　Data display and summary. In: Statistics at Square One. 9th Ed (Revised by MJ Campbell.): BMJ Books, 1996.

12. Altman DG, Royston P. The cost of dichotomising continuous variables.　BMJ. 2006;332:1080.

13. Kirkwood BR, Sterne JAC.　Essential Medical Statistics, 2nd　ed. Blackwell; 2003.

14. McHugh ML. The Chi-square test of independence. Biochem Med (Zagreb). 2013;23:143-9.

15. Trajman A, Luiz RR. McNemar test revisited: Comparing sensitivity and specificity of diagnostic examina-tions.　Scand J Clin Lab Invest. 2008,68:77-80.

16. Swinscow TDV.　The Chi-squared tests. In: Statistics at Square One. 9th Ed (Revised by MJ Campbell) BMJ Books, 1996.

17. Jeyaseelan L. Short Training Course Materials on Fundamentals of Biostatistics, Principles of Epidemiology and SPSS. CMC Vellore: Biostatistics Resource and Training Center (BRTC); 2007.

18. Mishra P, Pandey CM, Singh U, et al. Descriptive statistics and normality tests for statistical data.　Ann Card Anaesth. 2019;22:67-72.

19. Norman G. Likert scales, levels of measurement and the "laws" of statistics.　Adv Health Sci Edu. 2010;15:625–32.

20. Rana RK, Singhal R, Dua P. Deciphering the dilemma of parametric and nonparametric tests. J Pract Cardiovasc Sci. 2016;2:95-8.

21. Fagerland, MW. t-tests, non-parametric tests, and large studies - A paradox of statistical practice? BMC Med Res Methodol. 2012;12:78.