A. Indrayan
L. Satyanarayana*
From the Division of Biostatistics and
Medical Informatics, University College of Medical Sciences,
Dilshad Garden, Delhi 110 095, India and *Institute of Cytology
and Preventive Onco-logy, Maulana Azad Medical College Campus,
New Delhi 110 002, India.
Reprint requests: Dr. A.
Indrayan, Professor of Biostatistics,
Division of Biostatistics and Medical Informatics, University
College of Medical Sciences, Dilshad Garden, Delhi 110 095,
India.
We earlier defined biostatistics as the science
of management of uncertainties in health and disease(1). In the
previous articles of this series(2,3), we also included the
numerical and graphical methods to summarize data. The sheet
anchor of all this is the measure-ment because it is through
measurements that quantities are obtained, and variations and
uncertainties aptly studied. Thus, biostatistics can also be
perceived as the quantitative aspects of health and disease. The
qualitative aspects such as symptoms and relief are more important
in evaluating an individual’s health but that is the domain of a
clinician.
Some quantitative measures commonly used for
assessing the health of a child are Apgar score, respiration rate,
body temperature, and weight for age. Measurements are used not
only in assessing the levels of health and its various components
but also in assessing the disease severity. One example is Yale’s
observation scale(4) which is used to identify serious illness in
febrile children. Measurements are also used in establishing and
interpreting the reference values of various medical parameters,
in evaluating probailities in diagnosis and patient management, in
assessing the validity of medical tools, etc.
The usual practice in medicine is to evaluate
various parameters of a subject against a single or a range of
reference values. The methodology generally used to delineate such
reference values as well as their implications are discussed in
Section 6.1. Because of variations and un-certainties, this
assessment is done in terms of probabilities. These are discussed
in Section 6.2. Section 6.3 is on assessment of validity of
diagnostic tests.
6.1 Reference Values
Reference values are extensively used for
decisions on managing patients. It is known that the normal body
temperature in humans is 98.6° F and an Apgar score of 8 or more
is considered normal. A birth weight of <2.5kg is con-ventionally
considered low. A ponderal index [(weight in g/length in cm3)
*100] ³2.5
is considered normal in neonates and a child with index < 2.0
is classified as low ponderal index. The anthropometric
measurements are assessed by the percentile point achieved by a
child relative to the healthy children of that age and gender in
the same population. Median is regarded as a reference value, and
3rd and 97th percentiles as the thresholds to indicate abnormally
low and abnormally high values.
Weight for age and height for age are the most
commonly used indicators to assess growth but are more effective
when the trend over age for the same child is studied. The
interpretation and comparison of anthropometric measurements with
reference values is some-times performed by computing an index
called Z-score. This for weight is given by
Z–score = (Weight – Median)/SD
where Median and SD are calculated for the
reference healthy population of that age or of that height. A Z–score
below –2 is considered low and below –3 very low.
The other index used to assess growth is
"percent of median". A measurement below 80% of median
is regarded to indicate under-nutrition of Grade I; below 70%, of
Grade II; below 60%, of Grade III; and below 50%, of Grade IV. For
weight measurement, a velocity of less than normal for a younger
age group indicates failure to thrive. Recently, a 3-in-1 weight
monitoring chart for infants has been developed(5). Velocity is
the rate of growth per unit of time. This is higher at the
beginning of life and tapers off as age increases, with a slight
upswing at 6 or 7 years and a spurt in adole-scence. Preece and
Brans(6) have developed models that can be used to evaluate height
parameters such as age at take-off and peak height velocity.
The above discussion indicates that the
measurements are evaluated against reference or normal values. The
evaluation can be less risky and more meaningful if the basic
principles of establishing such normals are known.
Establishment of normals needs an understanding
of the distributional aspects of the measurements. You may like to
revisit a previous Article of this series(3) and refresh yourself
with the frequency distribution of measurements along with their
histogram, frequency polygon and frequency curve. The shape of the
distribution of a measurement such as birth weight in healthy
babies is nearly symmetrical. The frequencies are high in the
center and they rapidly decline on either side in almost a similar
fashion. The measurements such as cholesterol level, serum iron
and blood pressure (BP) in healthy subjects also tend to follow a
symmetric shape, called Gaussian.
Gaussian Distribution
This distribution is symmetric about mean and
has a shape of a bell. The shape of the curve is as shown in Fig.
1 for the distribution of serum iron in healthy adults. This
has the properties such as (i) mean, median and mode
coincide, and (ii) the limits from (mean - 2 SD) to (mean +
2 SD) cover the measurements of nearly 95% subjects. Such a
distribution is also called "normal distribution" but we
avoid using this term because normal has a different meaning in
medicine.
While many medical measurements in healthy
subjects do indeed follow a Gaussian pattern, all do not. The
distribution of blood lipids in children has a long tail on the
right because higher level is more common than lower level. This
is called a right-skewed distribution. On the other hand, the
distribution of hemoglobin level is generally left-skewed because
lower values are quite common. Fig. 2 shows the
age-distribution of deaths in a population of a developing
country. This has a bathtub shape and is entirely different from a
Gaussian pattern.
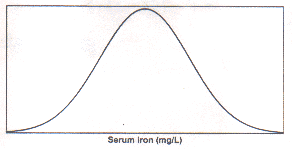
Fig1. Distribution of serumiron in healthy subjects (smothened
curve)
Normal or Reference Values
In this series, we use the two terms–reference
value and normal value–inter-changeably for values generally
seen in healthy subjects. The reference values could be separate
for different segments of the population. A level of BP seen
normally in adults would not be normal for children. A normal
weight of 2-year olds in Sudan may not be the same as normal
weight of 2-year olds in Sweden. Normals may also change from time
to time.
The normal values or reference values are based
on measurements of healthy subjects, preferably the most healthy
segment of the population. Generally, not less than 200 subjects
should be included in each group for which normal values are to be
obtained. Normal values are obtained generally by mean but
sometimes also by median and mode. See our previous Article(2) for
situations where median is preferable or mode is preferable. When
the inter-individual variation in healthy subjects is large, a
single normal value is not sufficient and we need a range of
normal values.
Normal Range
Even though normal is the level generally seen
in healthy subjects, there would always be persons with very high
or very low values yet absolutely healthy. The usual practice in
such cases is to exclude 2.5% subjects on either side from the
range of normality. This is arbitrary and purely statistical but
has become a con-vention in the absence of any other acceptable
criterion.
When the distribution is Gaussian, property-(ii)
is invoked to say that (mean –2 SD, mean +2 SD) are the normal
limits. They exclude 2.5% subjects with extreme measurements on
either side from the range of normality. These are popularly known
as ±2SD limits. Most of the normal ranges used in medical
practice are obtained in this manner. In case of birth weight, if
the mean in healthy babies in a population is 3.3 kg and SD 0.2
then the normal range is 2.9 kg to 3.7 kg for that population.
The use of ±2 SD limits as reference is not
without risk. These limits in any case exclude those 5% of healthy
subjects who have very low or very high values. In addition, many
subjects with disease may have values well within a normal range. Fig.
3 illustrates this overlap. This figure incidentally also
illustrates the wider dispersion generally seen among the diseased
subjects compared to the healthy subjects. This overlap gives rise
to false positivity and false negativity about which we discuss in
Section 6.3. Thus there is always a risk of misdiagnosis and
missed diagnosis in marginal cases. Such risk or uncertainty is
measured as follows.
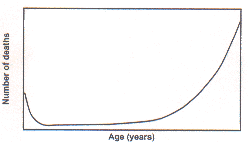
Fig2. Distribution of deaths by age at death in a developing
country
6.2 Measurement of Uncertainty
An accepted measure of uncertainty is
probability. The term has everyday meaning but its computation
could be nerve-wrecking in some intricate cases. Mathematically
speaking, an event which is impossible to occur, such as human
male giving birth to a child, has a probability zero. The event
which is certain to occur, such as death, has probability one.
Statistical definition is based primarily on empiricism and thus
is milder. If a women of age 54 years has never been seen to
conceive in the history of a community, the statistical
probability of occurrence of such an event in that community is
zero. It does not necessarily imply that the event is an
impossibility. No probability could be negative nor can it exceed
one. Probabilities have extensive usage in medicine. When the
first heart transplantation was done, the chances of success were
rated as 80%. The probability of recovery of a patient of tetanus,
after manifestation, is less than 50%. The chance of one year
graft survival of children with renal transplantation is 80%(7).
Thus probabilities have extensive usage.
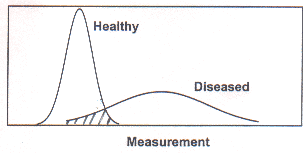
Fig. Overlap of values in healthy and diseased subjects.
Probability measures the likelihood of an event
and is complementary to uncertainty. An interpretation of
probability is the relative frequency of an outcome in a large
number of cases. This can be stated as
Probability of an outcome = Number of
cases with the desired outcome / Total number of cases
If the records of a community show that the
occurrence of Down syndrome is 1 in 700 live births, then the
probability of that complaint is 1/700 = 0.0014. Similarly,
probability of occurrence of one or more diseases together can
also be computed. Some laws of probability are helpful in this
context.
Laws of Probabilities
Occurrence of blindness and deafness in a child
are independent events in the sense that occurrence of one does
not increase or decrease the chance of occurrence of the other.
For such independent events, the joint probability of the two
occurring together in a child can be easily computed by the
product of the individual probabilities. Thus P (blindness and
deafness) = P (blindness) ´
P (deafness). This is called law of multiplication of
probabilities.
After corrective surgery for residual paralysis
in paralytic polio, the recovery could be full, partial or none.
In such mutually exclusive categories, the probability of belong-ing
to one or the other is computed by the law of addition. That is,
P (full or partial recovery) =P (full recovery) + P (partial recovery).
If the probability of full recovery is 0 . 30
and of partial recovery 0.40 then the probability of at least some
recovery is 0.70.
Probabilities in Diagnosis
We find diagnosis an easy portal for
communicating the concept of probability. But the usage in other
clinical activities is equally common.
Sometimes diseases are described in the
literature in the form of complaints commonly seen in that
disease. The track then is from disease to complaints. The actual
diagnostic process is just the reverse, from complaints to the
disease. Suppose the analysis of records show that 60% children of
tuberculous meningitis (TBM) presented with complaints of fever,
altered sensorium and convulsions. Then P (fever, altered
sensorium, convulsions/TBM) = 0.60, where P denotes probability.
Because of restriction to a specific group, which is mentioned
after the slash (/) sign, such probability is called conditional
probability. Note that this probability of signs and symptoms in a
particular disease is of very little value to a clinician. The
inverse probability, P (TBM/fever, altered sensorium, convulsions)
is useful because it gives the diagnostic value of the complaints.
Bayes’ rule helps to calculate the latter probability from the
former.
Use of Bayes’ rule: The probabilities
actually required in practice such as P (disease/complaints) can
be obtained from P (complaints/disease) using Bayes’ rule. This
is given below.
P (Disease/Complaints) = P (Complaints/Disease)
X
P (Disease) / P (Complaints)
P (Disease) is the prevalence of the disease in
the subjects under investigation. This is generally available from
various reports or books, or can be derived from records. The
second is P (Complaints) which is the relative frequency of the
complaints in the subjects. Special efforts may have to be made to
compute this. Once these two are known, the required inverse
probability can be calculated. For example, P (Infant death/Low
birth weight) can be computed from P (Low birth weight), say
23.5%, P (Low birth weight/Infant death), say 30.4% and P (Infant
death), say 5.9%. The required probability of infant death in
children with low birth weight (LBW) then is given by
P (Infant death/LBW) = P (LBW/Infant death) * P (Infant death) /
P (LBW)
This in this case is (0.304 ´ 0.059)/0.235
= 0.076 or 7.6%. Note that this is very different from P (LBW/Infant
death).
6.3 Validity of Diagnostic Tests
The tools used for evaluation and management of
health and disease are seldom perfect. They produce correct
results in many cases but not in all the cases. The ability of a
tool or of a procedure to correctly perform its assigned function
is called its validity. A valid diagnostic test would correctly
detect the presence as well as the absence of the disease. For
more details of this concept refer to Griner et al.(8).
Some tests are more valid than others though they may be more
expensive also. Western Blot is considered more efficacious than
ELISA in detecting HIV positivity. In contrast to blood culture,
the C-reactive protein (CRP) is utilized as a rapid diagnostic
test for septicemia in children. Fine needle aspiration cytology (FNAC)
for tissue diagnosis is nearly as valid as tissue biopsy.
Malaria is characterized by high fever with
chills and rigors, splenomegaly and a positive blood smear. How
valid is this set of criteria? Can it correctly identify all the
cases of malaria and can it correctly exclude all the non-malarial
cases? We discuss these two aspects in the following paragraphs.
Sensitivity and Specificity
The ability of a test to give positive results
in true cases of diseases is called sensitivity. Specificity is
the ability to give negative results in cases not suffering from
the disease. These are two components of validity of a test. The
components are best illustrated with the help of an example.
Example 1: In rural areas, where measuring
weight is not feasible due to logistic problems, an alternative
measure is mid-arm circumference (MAC). This is considered age and
sex independent for detecting malnutrition between the ages 12-60
months. MAC was measured for 453 children of preschool age(9).
They were also assessed for grade of malnutrition by weight for
age criteria. MAC was used as a test criteria for detecting
malnutrition with weight for age as the gold standard. The results
obtained are recorded in Table I. The following can be
noted.
True positives (TP) = 45
False positives (FP) = 67
True negatives (TN) = 330
False negatives (FN) = 11
Sensitivity and specificity can be calculated
as:
Sensitivity =TP / TP + FN,
and Specificity =TN /
TN + FP
Both can be converted to percentage by
multiplying by 100. Sensitivity and speficity of MAC against
weight for age are 0.804 and 0.831 respectively. These are
converted as percentages and shown in Table I.
Predictivity
The actual problem in practice is to detect the
presence or absence of a suspected disease by using a test. The
diagnostic value of a test is measured by the probability of
presence of disease among those who are test positives, and the
probability of absence of disease among those who are test
negatives. These indicators are called positive predictivity and
negative predictivity respectively. These are also called
post-test probabilities.
In terms of notations,
Positive predictivity = TP / TP + FP
and Negative predictivity =TN / TN + FN
Predictivities are severly affected by the
prevalence of disease among those tested.On the other hand,
sensitivity and specificity are absolute and do not depend on
prevalence. The predictivities for some specific values of
sensitivity and specificity, and for different prevalences are
shown in Table II. As the prevalence increases the positive
predictivity also increases and this increase is more pronounced
when specificity is low. Higher prevalence leads to less negative
predictivity, more so when sensitivity is low. In summary, the
calculation of predictivities should be done on subjects that
correctly represent the propor-tion of diseased and non-diseased
cases among those who are to be tested.
The dependence of predictivities on the
"prevalence" is to be cautiously interpreted. This
prevalence is among those who are administered the test. A
diagnostic test is generally adminis-tered to those who are
suspected to have the disease and in them, the proportion with
disease is likely to be high. This proportion is the same as
prevalence in the sense used here. When this is high, it becomes
difficult to correctly identify the negatives.
Another very useful interpretation of
prevalence is the extent of belief or of confi-dence that a
clinician has in a particular subject for the presence of disease.
On the basis of the information available on the subject before
the test, if a clinician evaluates that the chance of disease in
that subject is 60% then this has exactly same connotation as
prevalence. Thus prevalence can also be understood as the pre-test
probability. Predictivities can be assessed using this probability
in place of prevalence.
|
Table I -
Mid-arm Circumference in Identification of Malnutrition
|
| Malnutrition as per
for age percent of reference median |
Malnutrition as per mid-arm circumference |
| £
12 cm (+) |
> 12
cm (–) |
Total |
| |
TP
|
FN
|
|
| 60% (+) |
45 |
11 |
56 |
| > 60% (–) |
67 |
330 |
397 |
| Total |
112 |
341 |
453 |
Sensitivity: 80.4%
|
Specificity: 83.1%
|
|
|
| Source: Mohan et al.(9).
|
|
Table II -
Predictivities
for Some Specific Values of Sensitivity, Specificity and
Prevalence
|
| SensitivityS (+) |
|
Prevalence
|
Predictivity (%) |
Specificity
S
(–) |
|
Positive
P (+) |
NegativeP
(–) |
| 0.20
|
0.20
|
0.10
|
3
|
69
|
| |
|
0.50
|
20
|
20
|
| |
|
0.90
|
69
|
3
|
| 0.20
|
0.90
|
0.10
|
18
|
91
|
| |
|
0.50
|
67
|
53
|
| |
|
0.90
|
95
|
11
|
| 0.90
0. |
20
|
0.10
|
11
|
95
|
| |
|
0.50
|
53
|
67
|
| |
|
0.90
|
91
|
18
|
| 0.90
|
0.90
|
0.10
|
50
|
99
|
| |
|
0.50
|
90
|
90
|
| |
|
0.90
|
99
|
50
|
1. Indrayan A, Satyanarayana L. Essentials of
Biostatistics: 1. Medical uncertainties. Indian Pediatr 1999; 36:
471-477.
2. Indrayan A, Satyanarayana L. Essentials of
Biostatistics: 4. Numerical methods to summarize data. Indian
Pediatr 1999; 36: 1127-1134.
3. Indrayan A, Satyanarayan L. Essentials of
Biostatistics: 5. Graphical methods to summarize data. Indian
Pediatr 1999; 37: 55-62.
4. McCarthy PL, Sharpe MR, Spiesel SZ, Dolan TF,
Forsyth BW, DeWitt TG, et al. Observation scales to
identify serious illness in febrile children. Pediatrics 1982; 70:
802-809.
5. Cole TJ. 3-in-1 weight-monitoring chart.
Lancet 1997; 349: 102-103.
6. Preece MA, Baines MJ. A new family of
mathematical models describing the human growth curve. Ann Hum
Biol 1978; 5: 1-24.
7. Ramprasad KS, Hariharan S, Gopalkrishnan G,
Pandey AP, Jacob CK, Kirubakaran MG, et al. Renal
transplantation in children. Indian Pediatr 1987; 24: 1069-1072.
8. Griner PF, Mayewski RJ, Mushlin AI,
Greenland P. Selection and interpretation of diagnostic tests and
procedures: Principles and applications. I. Principles of test
selection and use. Ann Intern Med 1981; 94 (4PT2): 557-592.
9. Mohan M, Ramji S, Satyanarayana L, Marwah J, Kapani V. Thigh
circumference in assessing malnutrition in preschoold children.
Indian Pediatr 1988; 25: 255-257.
|
